Lernaufgabe 6: Kondensatoren
Hier findest du die Lösungen.
Eingangsexperiment
Aufgebaut wird folgende Schaltung:
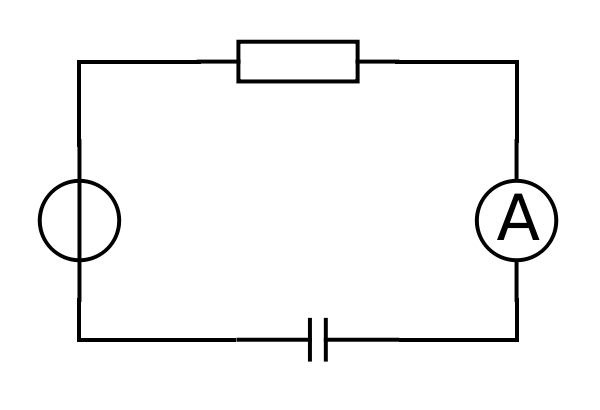
Die Spannungsquelle kann sowohl Gleich- als auch Wechselspannung liefern.
Versuch 1: Die Schaltung wird mit Gleichspannung versorgt und der Strom gemessen.
Versuch 2: Die Schaltung wird mit einer Wechselspannung gleicher Höhe versorgt und der Strom gemessen.
Bevor der Versuch durchgeführt wird entscheide dich für eine der folgenden Vermutungen:
1) Der Strom bei Gleichspannung ist geringer als bei Wechselspannung.
2) Die Höhe des Stroms bleibt gleich, egal ob Gleich- oder Wechselspannung.
3) Der Strom bei Gleichspannung ist höher als bei Wechselspannung.
Arbeitsauftrag: Erarbeite das Verhalten eines Kondensators im Wechselstromkreis.
Material:
- Fachbuch Kapitel 7.5.1: Kapazitiver Blindwiderstand
Im Verlauf der Erarbeitung beantworte die folgenden Aufgaben.
Aufgabe 1
Gib das Schaltzeichen eines Kondensators an.
Aufgabe 2
Benenne die Ursache für den höheren Stromfluss eines Kondensators an Wechselspannung als bei Gleichspannung.
Aufgabe 3
Vervollständige den folgenden Satz:
Ein Kondensator im Wechselstromkreis hat einen \(\underline{\qquad\qquad\qquad\qquad}\), der durch \(\underline{\qquad\qquad\qquad\qquad}\) entsteht.
Aufgabe 4
Der regelmäßige Wechsel der Spannungsorientierung führt zu einem steten Auf- und Entladen des Kondensators. Dieses Auf- und Entladen führt zu einem Stromfluss \(I>0\). Bei einem idealen Kondensator (keine Leckströme) erreicht die Kondensatorspannung \(U_\mathrm{bC}\) ihren Scheitelwert jeweils eine Viertelperiode (\(90^\circ\)) später als der Strom \(I\).
Vervollständige den Satz:
Im kapazitiven Blindwiderstand eilt der Wechselstrom der Wechselspannung um 90° \(\underline{\qquad\qquad\qquad}\).
Aufgabe 5
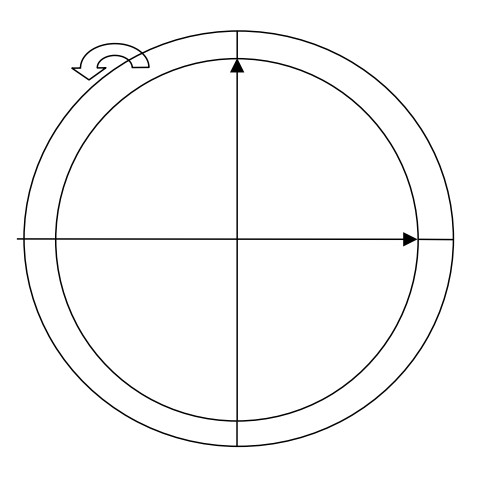
Trage den Strom- und Spannungszeiger (\(I\) und \(U_\mathrm{bC}\)) eines idealen Kondensators in das Zeigerbild ein.
Wenn ein Zeigerbild noch Neuland sein sollte, so recherchiere vorher, was ein Zeigerbild ist.
Aufgabe 6
Gib das Formelzeichen, die Einheit und die Formel zur Berechnung des kapazitiven Blindwiderstandes an.
Aufgabe 7
Die Kapazität \(C\) ist ein Maß für die Höhe der gespeicherten Ladung auf den Kondensatorplatten. Auch die Frequenz \(f\) hat einen Einfluss auf den Blindwiderstand.
Trage in die folgende Tabelle die Wirkung auf den Blindwiderstand ein.
| Veränderung | Wirkung auf \(X_C\) |
|---|---|
| Kapazität \(C\) \(\uparrow\) | |
| Kapazität \(C\) \(\downarrow\) | |
| Frequenz \(f\) \(\uparrow\) | |
| Frequenz \(f\) \(\downarrow\) |
Aufgabe 8
Gib das Formelzeichen und die Einheit der Kapazität an.
Aufgabe 9
Widerstände in Reihen- oder Parallelschaltung können durch Ersatzwiderstände zusammengefasst werden. Gleiches ist mit Kapazitäten möglich.
Finde die Formeln, welche die Zusammenfassungen von Kapazitäten ermöglichen.
Aufgabe 12
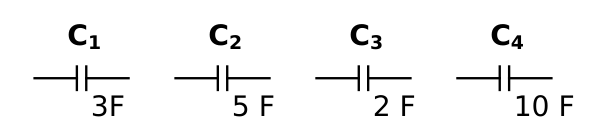
Berechne folgende Gesamtkapzitäten \(C_\mathrm{ges}\) unter Anwendung der gefundenen Formeln:
1) \(C_1, C_2, C_3\) in Reihe
2) \(C_1,C_2,C_3\) parallel zueinander
3) \(C_4\) in Reihe mit der Parallelschaltung von \(C_1, C_2, C_3\)